Of course, you're thinking, "Wait! Calculus was invented by Newton and Leibnitz in the 17th century!"  That is, of course correct, but it brings to mind a famous moment from the Star Trek episode, "Whom Gods Destroy."

Dr. Garth: "You wrote that?"

Marta: "Yesterday, as a matter of fact."

Dr. Garth: "It was written by an Earth man named Shakespeare a long time ago!"

Marta: "Which does not alter the fact that I wrote it again yesterday!"

Sure, calculus had been invented for a long time, but when I was in seventh grade, I didn't know that.  I just knew I had something cool.

It was like the moment in the early 1980s when I was writing a cross-assembler for the Texas Instrument 32032 microprocessor, which the world missed out on realizing was the sweetest piece of silicon on the planet at the time, kicking both Intel and Motorola into the Outer Darkness.  I hated the idea of writing the same code over and over and over, so I hit upon an idea of using structures with method pointers and embedded data, and implemented a way to copy one structure to another and change the method pointers as needed.  It was super!  It was awesome!  It was mind-blowingly magic!  I knew I had come up with an unbelievably powerful methodology that could change the whole scene of software development.

What I didn't know was that it was object-oriented programming and that it already existed, but just barely.  I recall reading an article in Byte magazine about it around that time, but the author was so in love with the Smalltalk language that he spent the whole thing talking about message-passing and run-time binding and virtually neglected to mention what OO programming is all about.  Otherwise I would have recognized it.  I had it all: encapsulation, polymorphism, inheritance.  (If some tells you that you can't do object-oriented programming in assembly language, proceed to laugh at him.)

But that moment reminded me of the time in seventh grade.

I remember where I was sitting: second row, right of center.  It was in English class, and that was before I understood that English was cool, too.  So naturally, instead of listening, I sat there playing with math.  They had taught us in science (or I picked it up in a book — I did understand the importance of reading) about simple machines.  Levers in particular.  I realized that what they taught you in junior high was simple enough as long as you had a fundamental shape where you could figure out the center of mass, but suppose you didn't?  Suppose you had a see-saw with an irregular load of dirt on one side.  Just what do you do then, huh?

But that just made it a more interesting challenge to distract me from grammar.  I reasoned that if  you chopped up that load of dirt into segments and estimated the center of mass for each one and added up the effect of them all, you'd get a fair approximation of the answer.  I reasoned further that if you made the chunks smaller and smaller until you had an infinite number of zero-sized chunks, you'd get the exact answer.  I reasoned at last that if you had a formula (we hadn't learned about functions yet, either) that expressed how much dirt you had at each position along the length, then you could do it all on paper.

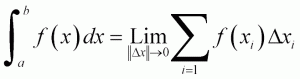So, what I had was what in college we call a limit of Reimann sums of function segments.  The figure shows how we define a Reimann integral today.  There you have it.  The limit of sums of a function evaluated at specific points.  That the size of the largest increment has to go to zero instead of simply the number of increments going to infinity is a detail I missed in seventh grade.  I had just assumed all the segments would be the same width.

It seems like I didn't get very far in actually calculating integrals then.  If my memory serves, I sort of lost interest in that particular problem before figuring out how to calculate the limits.  But I had the concept, and it sure made calculus easier when, a year later, I found a book on it in a discount table at Kresge's (the predecessor of K-mart) and started teaching myself.  It was the best 63 cents I've ever spent.

So why am I telling you all this?  Probably frustration!

That was pretty good for a 13-year-old at the time.

I just wish I was that smart now!!!!!